Soal & Pembahasan UN Matematika SMP 2016 (Bagian 3)
SOAL & PEMBAHASAN UN MATEMATIKA SMP 2016 (BAGIAN 3)
Hello my dear...
Hahaha... atiek ki ngomong opo...
Halo halo teman, Gimana belajarnya? Semoga Lancar Jaya. Aamiin
Pada kesempatan sebelumnya kita telah bahas Soal & Pembahasan UN Matematika SMP (Bagian 2). Selanjutnya kita lanjutkan bahasan Soal & Pembahasan UN Matematika SMP (Bagian 3). Oke lanjut ya...
Pembahasan

(Jawaban C)
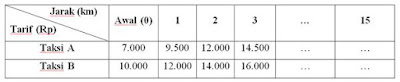
18. “Tarif Taksi”
Sebuah kota terdapat dua perusahaan taksi A
dan taksi B.
Perusahaan tersebut menawarkan tarif taksi
seperti tabel.
Penumpang taksi (konsumen) dapat memilih
tarif taksi yang lebih murah. Yunia ingin pergi ke Mall yang berjarak 15 km dari rumahnya. Agar diperoleh biaya yang
lebih murah, taksi manakah yang sebaiknya akan digunakan oleh Yunia?
A. taksi A, karena tarif taksi yang lebih
murah
B. taksi B, lebih murah karena lebih kecil,
sehingga akan terus murah
C. taksi B, karena lebih murah 4.000 rupiah
D. taksi B, karena lebih murah 4.500 rupiah
Pembahasan
Berdasarkan dari tabel diketahui:
Tarif taksi A bermula 7.000 dan akan
meningkat 2.500 setiap km nya. Jadi pada kilometer ke-15 (suku ke-16, karena
dimulai dari 0 km) tarif taksi A adalah
7.000 + (16 – 1)2.500 = 44.500
(Ingat rumus suku ke-n dari barisan
aritmatika adalah a + (n – 1)b
Tarif taksi B bermula 10.000 dan akan
meningkat 2.000 setiap km nya. Jadi pada kilometer ke-15 (suku ke-16, karena
dimulai dari 0 km) tarif taksi B adalah
10.000 + (16 – 1)2.000 = 40.000
Jadi, Yunia sebaiknya naik taksi B, karena
lebih murah 4.500 rupiah
(Jawaban D)
Pembahasan
Antara tangga dengan lantai dan tembok
membentuk segitiga siku-siku di perpotongan tembok dengan lantai. Dengan
demikian untuk mencari tinggi tembok dapat dicari dengan Teorema Pytagoras.
Jika dimisalkan tinggi tembok adalah x,
maka:
jadi, kemiringan tembok adalah
(Jawaban B)
Pembahasan
Ingat rumus persamaan garis yang melalui (x1, x2)
dengan gradien m adalah (y
– y1) = m(x
– x1)
(y – 3) = -2(x – 4)
y
– 3 = -2x + 8
y
+ 2x – 11 = 0
(Jawaban A)
21. Persamaan garis b seperti tampat pada gambar adalah …
A. 2y
= x – 1
B. 2y
= -x – 1
C. 2y
= x + 1
D. 2y
= -x + 1
Pembahasan
Berdasarkan dari gambar garis a tegak lurus dengan garis b, dan
Garis b
melalui (-1, 0)
Gradien garis a (yang melalui titik (-1, 0) dan (0, 2)) adalah
Dengan demikian gradien garis b adalah
Sehingga persamaan garis b yang melalui (-1, 0) dan bergradien – ½ adalah
(y
– 0) = - ½ (x – (-1))
y = - ½ x – ½
2y
= -x – 1
(Jawaban B)
22. Seorang tukang parkir mendapat uang
sebesar Rp 17.000,00 dari 3 buah mobil dan 5 buah motor, sedangkan dari 4 buah
mobil dan 2 buah motor ia mendapat uang Rp 18.000,00. Jika terdapat 20 mobil
dan 30 motor, banyak uang parker yang ia peroleh adalah …
A. Rp 135.000,00
B. Rp 115.000,00
C. Rp 110.000,00
D. Rp 100.000,00
Misal: parkir satu mobil a dan parkir satu motor b
Sehingga,
3a
+ 5b = 17.000 ½× 4 ½12a + 20b = 68.000
4a
+ 2b = 18.000 ½× 3 ½12a + 6b = 54.000
14b
= 14.000
b
= 1.000
substitusikan b = 1.000 ke 3a + 5b = 17.000, didapatkan
3a
+ 5(1.000) = 17.000
3a
+ 5.000 = 17.000
3a
= 12.000
a = 4.000
Jadi, parkir 20 mobil dan 30 motor adalah
20 × 4.000 + 30 × 1.000 = 80.000 + 30.000 =
110.000
(Jawaban C)
Pembahasan
ÐKLN + ÐMLN = 1800
(3x
+ 15) + (2x + 10) = 180
5x
+ 25 = 180
5x
= 180 – 25 = 155
x = 31
Sudut pelurus KLN adalah sudut MLN, yaitu
2x
+ 10 = 2 × 31 + 10 = 62 + 10 = 72
(Jawaban B)
Pembahasan
ÐBAC + ÐACB = ÐCBD
(y
+ 10) + (2y + 10) = 140
3y
+ 20 = 140
3y
= 120
y = 40
ÐBAC = y + 10 = 40 + 10 = 50
(Jawaban C)










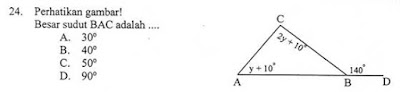



Komentar
Posting Komentar